Determinants ریاضی کا ایک اہم موضوع ہے جو مختلف طبیعیات اور انجینئرنگ کے مسائل کو حل کرنے میں مددگار ثابت ہوتا ہے۔ اس کی سمجھ بوجھ حاصل کرنا نہ صرف ریاضی کی مبادیات کو بہتر بناتا ہے بلکہ مختلف قسم کی مساوات کو حل کرنے میں بھی کارآمد ہے۔
Determinants کو حل کرنے کے طریقے سیکھنا طلباء کے لیے فائدہ مند ہوتا ہے، خاص طور پر جب وہ میٹرکس کے مختلف پہلوؤں پر کام کر رہے ہوں۔ اس مضمون میں، ہم Determinants کے حل کے بنیادی طریقوں پر روشنی ڈالیں گے، جو آپ کو مزید پیچیدہ مسائل حل کرنے میں مدد دے گا۔
دا determinant کی اقسام
جب ہم determinants کی بات کرتے ہیں، تو ہمارے ذہن میں اکثر مختلف اقسام آتی ہیں۔ ہر قسم کا اپنے مخصوص اطلاق اور خصوصیات ہیں۔ آئیے، ان اقسام کی تفصیل میں جاتے ہیں:
1. 2x2 Determinant
یہ سب سے بنیادی اور عام قسم کا determinant ہے۔ یہ صرف 2 صفوں اور 2 کالموں پر مشتمل ہوتا ہے۔ اس کی فارمولا یہ ہے:
Det(A) = ad - bc
جہاں A = |a b|
|c d|
اس قسم کے determinants کا استعمال بنیادی مسائل کے حل کے لئے بہت کیا جاتا ہے، جیسے کہ سادہ نظام کی مساواتیں۔
2. 3x3 Determinant
3x3 determinants تھوڑے پیچیدہ ہوتے ہیں اور ان میں 3 صفوں اور 3 کالم ہوتے ہیں۔ ان کا حساب کرنے کے لئے ہم عام طور پر *Sarrus Rule یا cofactor expansion کا استعمال کرتے ہیں۔ 3x3 determinants کے لئے فارمولا یہ ہے:
Det(A) = a(ei - fh) - b(di - fg) + c(dh - eg)
جہاں A = |a b c|
|d e f|
|g h i|
یہ determinant مختلف سائنس اور انجنئیرنگ کے مسائل کی تفہیم کے لئے بہت موثر ہوتا ہے۔
3. Higher Order Determinants
جب determinants کی صفیں اور کالم بڑھتے ہیں، جیسے کہ 4x4 یا 5x5، تو ان کی پیچیدگی بھی بڑھ جاتی ہے۔ اس لئے، ان کا حساب سیکھنا تھوڑا زیادہ وقت طلب ہو سکتا ہے۔ ان کا حساب کرنے کے لئے آپ Cofactor Expansion یا Row Reduction جیسے مختلف طریقوں کا استعمال کر سکتے ہیں۔
4. Special Determinants
کچھ determinants میں خاص خصوصیات ہوتی ہیں، جیسے:
- Diagonal Determinants: ان میں صرف diagonal عناصر ہوتے ہیں اور باقی سب صفر ہوتے ہیں۔
- Triangular Determinants: یہ determinants اوپر یا نیچے triangular شکل میں ہوتے ہیں۔ ان کا حساب بہت آسان ہوتا ہے۔
- Singular Determinants: ان کا determinant 0 ہوتا ہے، جو یہ دکھاتا ہے کہ یہ invertible نہیں ہیں۔
اس طرح، determinants کی یہ مختلف اقسام ہمیں نہ صرف ان کی پیچیدگی کو سمجھنے میں مدد دیتی ہیں بلکہ مختلف ریاضیاتی مسائل کے حل میں خصوصی طور پر اہم ثابت ہوتی ہیں۔
یہ بھی پڑھیں: How Much Does Music PR Cost in Urdu
Determinants کو حل کرنے کے طریقے
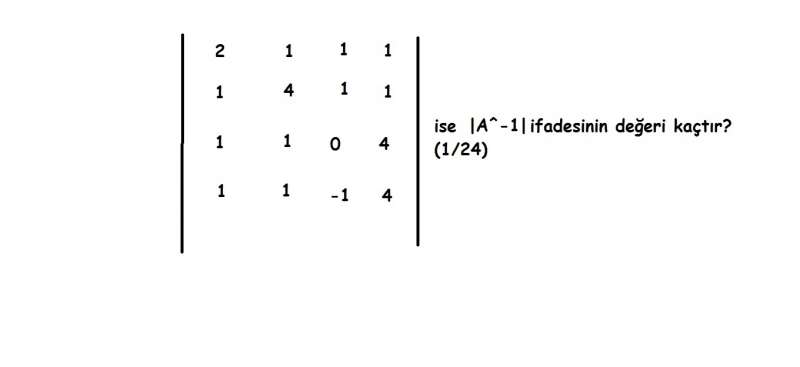
Determinants ریاضی میں ایک اہم تصور ہیں، خاص طور پر لائنئیر الجبرا کے شعبے میں۔ اگر آپ جاننا چاہتے ہیں کہ یہ کسے حل کیا جاتا ہے، تو یہاں کچھ بنیادی طریقے پیش کیے جا رہے ہیں:
یہ بھی پڑھیں: Desora Desloratadine Tablets کیا ہیں اور کیوں استعمال کی جاتی ہیں – استعمال اور سائیڈ ایفیکٹس
1. 2x2 Determinant کا حل
ایک 2x2 Determinant کو حل کرنے کا طریقہ انتہائی آسان ہے۔ اگر آپ کے پاس یہ میٹرکس ہے:
A =
a b
c d
تو Determinant کی فارمولا یہ ہے:
Det(A) = ad - bc
مثال کے طور پر، اگر:
A =
3 5
4 2
تو:
Det(A) = (3 2) - (5 * 4) = 6 - 20 = -14
یہ بھی پڑھیں: جامن کے صحت کے فوائد اور استعمالات اردو میں
2. 3x3 Determinant کا حل
3x3 Determinants کا حل کرنے کے لئے آپ کھیلو کی ترقی کر سکتے ہیں، جنہیں ہم minors اور cofactors کہتے ہیں۔ ایک 3x3 میٹرکس کی صورت میں:
B =
a b c
d e f
g h i
Determinat کا فارمولا یہ ہے:
Det(B) = a(ei - fh) - b(di - fg) + c(dh - eg)
یہ فارمولا آپ کو ایک مرتبہ میں تین 2x2 Determinants کو حل کرکے نتیجہ دے گا۔
یہ بھی پڑھیں: How to Reduce Man Boobs in Urdu
3. Laplace Expansion کا استعمال
اگر آپ کے پاس بڑی میٹرکس ہیں، تو Laplace Expansion ایک زیادہ موثر طریقہ ہے۔ آپ کسی بھی صف یا کالم کے انتخاب کے ذریعے Expande کر سکتے ہیں۔
یہ بھی پڑھیں: حسن یوسف پاؤڈر کے فوائد اور استعمالات اردو میں
4. Matrices اسٹیپرز کا استعمال
کچھ صورتوں میں، آپ مٹرکس کو row operations کے ذریعے بھی حل کر سکتے ہیں۔ اس میں میٹرکس کو triangular شکل میں لانا شامل ہے تاکہ Determinant آسانی سے نکالا جا سکے۔
ان طریقوں کے ذریعے آپ آسانی سے Determinants کو حل کر سکتے ہیں۔ یاد رکھیں کہ محنت اور مشق کے ساتھ آپ اس موضوع پر مہارت حاصل کر سکتے ہیں!
یہ بھی پڑھیں: Piracetam Syrup کیا ہے اور اس کے استعمال اور سائیڈ ایفیکٹس
مثالوں کے ذریعے سمجھنا
Determinants کو سمجھنا کبھی کبھار مشکل ہو سکتا ہے، لیکن چند مثالوں کے ذریعے ہم اسے آسانی سے سمجھ سکتے ہیں۔ آئیے شروع کرتے ہیں ایک سادہ مثال سے۔
یہ بھی پڑھیں: Neoprox 500mg کیا ہے اور کیوں استعمال کیا جاتا ہے – استعمال اور سائیڈ ایفیکٹس
مثال 1: 2x2 Determinant
چلیں ایک 2x2 میٹرکس لیتے ہیں:
\[ A = begin{pmatrix} a & b \ c & d end{pmatrix} \]
اس کے determinant کو تلاش کرنے کے لیے ہم اس فارمولا کا استعمال کرتے ہیں:
\[ text{det}(A) = ad - bc \]
فرض کریں:
\[ A = begin{pmatrix} 3 & 2 \ 1 & 4 end{pmatrix} \]
اب ہم determinant کا حساب لگاتے ہیں:
\[ text{det}(A) = (3 times 4) - (2 times 1) = 12 - 2 = 10 \]
اس طرح، اس میٹرکس کا determinant 10 ہے۔
یہ بھی پڑھیں: How to Make a Nice Presentation in Urdu
مثال 2: 3x3 Determinant
آئیے اب 3x3 میٹرکس کی ایک مثال دیکھتے ہیں:
\[ B = begin{pmatrix} 1 & 2 & 3 \ 0 & 4 & 5 \ 1 & 0 & 6 end{pmatrix} \]
اس میٹرکس کے determinant کو نکالنے کے لیے، ہم cofactor expansion کا استعمال کر سکتے ہیں:
\[ text{det}(B) = a_{ij} cdot C_{ij} \]
جہاں ( C_{ij} ) کی تعریف ہوتی ہے کہ یہ minor کا determinant ہے۔ چلیے پہلی سطر (first row) سے شروع کرتے ہیں:
- 1 سے متعلق minor: \[ C_1 = begin{vmatrix} 4 & 5 \ 0 & 6 end{vmatrix} = (4 times 6) - (5 times 0) = 24 \]
- 2 سے متعلق minor: \[ C_2 = begin{vmatrix} 0 & 5 \ 1 & 6 end{vmatrix} = (0 times 6) - (5 times 1) = -5 \]
- 3 سے متعلق minor: \[ C_3 = begin{vmatrix} 0 & 4 \ 1 & 0 end{vmatrix} = (0 times 0) - (4 times 1) = -4 \]
اب ہم determinant کا حساب لگا سکتے ہیں:
\[ text{det}(B) = 1 cdot 24 - 2 cdot (-5) + 3 cdot (-4) = 24 + 10 - 12 = 22 \]
اس طرح، 3x3 میٹرکس کا determinant 22 ہے۔
ان مثالوں کے ذریعے ہم نے سیکھا کہ determinats کا حساب لگانا کتنا آسان ہو سکتا ہے، بس تفصیل سے حساب کریں!
یہ بھی پڑھیں: اردو میں Itrifal Ustukhuddus کے فوائد اور استعمالات
Determinants کے فوائد
جب ہم Determinants کی بات کرتے ہیں، تو یہ صرف کچھ ریاضیاتی چیزیں نہیں ہیں، بلکہ ان کے کئی اہم فوائد بھی ہیں جو مختلف شعبوں میں مددگار ثابت ہوتے ہیں۔ یہاں ہم کچھ اہم فوائد کو جانچیں گے:
- ریاضی اور الجبرا میں اہمیت: Determinants کی مدد سے ہم میٹرکس کی منفرد خصوصیات معلوم کر سکتے ہیں۔ یہ ہمیں بتاتے ہیں کہ آیا کوئی میٹرکس invertible ہے یا نہیں۔
- حل کرنے کے طریقے: Determinants کا استعمال linear equations کو حل کرنے میں بھی ہوتا ہے، خاص طور پر Cramer’s Rule کے ذریعے، جو مخصوص حالات میں سہولت فراہم کرتا ہے۔
- جیومیٹری میں درخواست: جیومیٹری کے مسائل میں، Determinants ہم سب سے زیادہ کارآمد ثابت ہوتے ہیں، مثال کے طور پر، کسی مثلث کے رقبے کا حساب لگانے میں۔
- فزکس اور انجینئرنگ میں استعمال: Determinants کو فزکس میں مختلف پیمائشوں کے درمیان تعلق جاننے کے لیے استعمال کیا جاتا ہے، جیسے کہ Force اور Distance کے درمیان۔
یہ بھی پڑھیں: گووس بیری کے فوائد اور استعمالات اردو میں Gooseberry
Determinants کا کردار
Determinants کی اہمیت صرف ریاضی میں ہی نہیں بلکہ سائنس اور ٹیکنالوجی کے مختلف شعبوں میں بھی ہے۔ ان کی مدد سے ہم مختلف نوعیت کے مسائل کو سیدھے اور واضح طریقے سے حل کر سکتے ہیں۔
نتیجہ
آخری بات یہ ہے کہ Determinants صرف ایک ریاضیاتی آلہ نہیں ہیں، بلکہ یہ ہمارے لیے کئی اہم مواقع فراہم کرتے ہیں۔ چاہے آپ ایک طالب علم ہوں، ایک انجینئر، یا ایک محقق، Determinants آپ کے کام کو آسان بنا سکتے ہیں۔ ان کی خصوصیات اور فوائد کا گہرے سے مطالعہ آپ کو اپنی علمی مہارتوں میں اضافہ کرنے کا موقع فراہم کرتا ہے۔ لہذا، اپنی تحقیق میں Determinants کو شامل کرنے سے نہ گریز کریں! یہ آپ کی دلچسپیوں کو وسیع کرتے ہوئے نئے راستے کھول سکتے ہیں۔
