کس طرح Fractions حل کریں کے موضوع پر گفتگو کرتے ہوئے، ہمیں ان عددی تناسب کی اہمیت اور ان کے استعمال کی ضرورت کو سمجھنا ہوگا۔ Fractions ریاضی کے بنیادی اجزاء میں شامل ہیں اور مختلف عملی Anwendungen میں استعمال ہوتے ہیں، جیسے کہ کھانا پکانے، مالیات، اور تعمیرات۔
Fractions حل کرنے کے بنیادی طریقوں کا علم ہر کسی کے لیے ضروری ہے، خصوصاً طلباء کے لیے۔ اس مضمون میں، ہم مختلف تکنیکوں، قواعد، اور حکمت عملیوں کا جائزہ لیں گے تاکہ آپ آسانی سے Fractions کو حل کر سکیں۔ ان مہارتوں کے ساتھ، آپ ریاضی میں مزید آگے بڑھنے کے لیے تیار ہوں گے۔
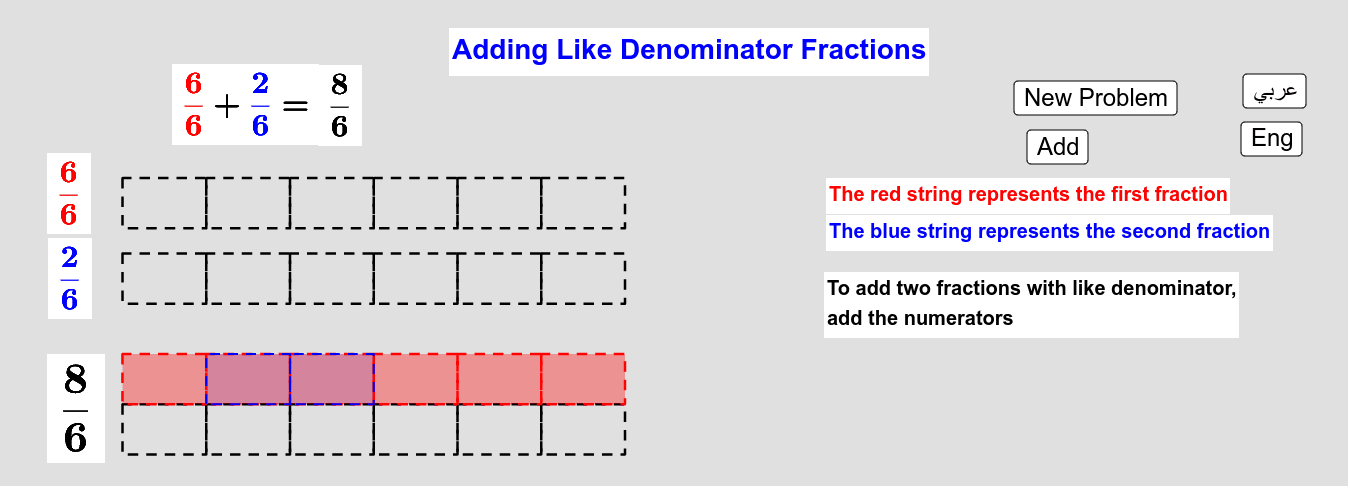
Fractions کو جمع کرنا
جب آپ *Fractions کو جمع کرتے ہیں، تو سب سے پہلے آپ کو بنیادی اصولوں کو سمجھنا ہوگا۔ یہاں پر ہم جائزہ لیں گے کہ آپ کیسے مختلف Fractions کو آسانی سے جمع کر سکتے ہیں۔
آئیے پہلے ایک مثال کے ذریعے سمجھیں۔ فرض کریں کہ ہمارے پاس دو Fractions ہیں:
- ¾
- ⅖
ان کو جمع کرنے کے لئے ہمیں چند مراحل سے گزرنا ہوگا:
یہ بھی پڑھیں: Cefiget 400mg کیا ہے اور اس کے استعمال اور سائیڈ ایفیکٹس
مرحلہ 1: مشترک بنیادی تعداد تلاش کریں
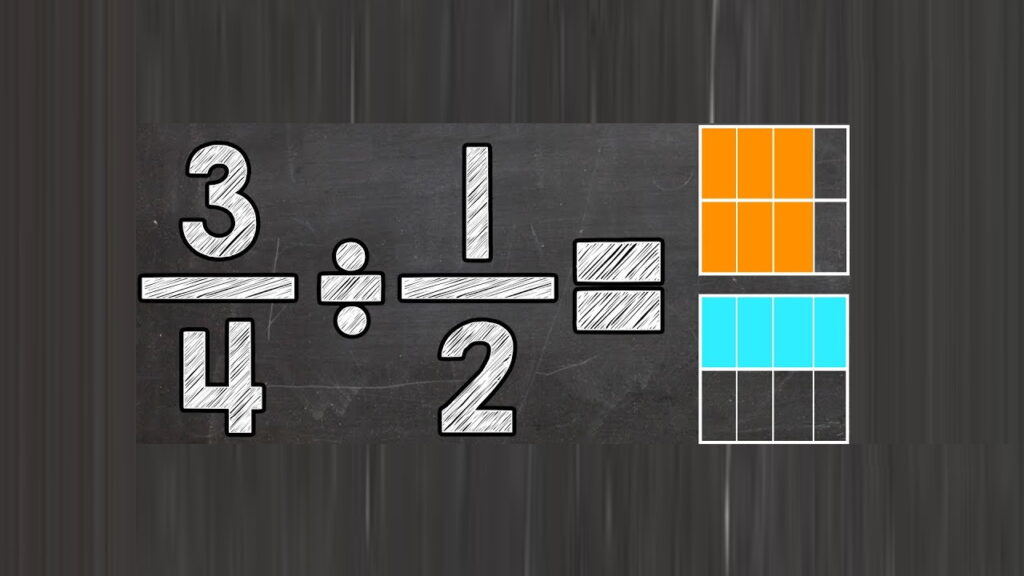
پہلا قدم ہے کہ دونوں Fractions کا مشترک بنیادی تعداد تلاش کرنا۔ ¾ اور ⅖ کے لئے مشترک بنیادی تعداد 12 ہے۔
یہ بھی پڑھیں: Breeky Tab کیا ہے اور اس کے استعمال اور سائیڈ ایفیکٹس
مرحلہ 2: Fractions کو برابر کریں
اب ہم دونوں Fractions کو مشترک بنیادی تعداد کے مطابق بدلیں گے۔
- ¾ = 9/12 (کیوں کہ 3 × 4 = 12 اور 4 کا 3 کے ساتھ ضرب دینے سے 9 آتا ہے)
- ⅖ = 6/12 (کیوں کہ 2 × 6 = 12 اور 6 کا 2 کے ساتھ ضرب دینے سے 6 آتا ہے)
یہ بھی پڑھیں: Phenotil Tablet کیا ہے اور اس کے استعمال اور سائیڈ ایفیکٹس
مرحلہ 3: Fractions کو جمع کریں

اب ہم دونوں کو جمع کرتے ہیں:
9/12 + 6/12 = 15/12
تو ہمارا نتیجہ ہے 15/12۔
یہ بھی پڑھیں: ککبٹر جوس کے فوائد اور استعمالات اردو میں Cucumber Juice
مرحلہ 4: سادہ شکل میں تبدیل کریں
اب ہمیں آخری جواب کو سادہ شکل میں پیش کرنا ہے۔ 15/12 کو ہم 1 1/4 میں تبدیل کر سکتے ہیں۔
خلاصہ: Fractions کو جمع کرنا تھوڑا سا مختلف ہو سکتا ہے، لیکن اگر آپ ان مراحل کا خیال رکھیں تو یہ آسان ہو جاتا ہے۔ یاد رکھیں:
- مشترک بنیادی تعداد تلاش کریں۔
- Fractions کو برابر کریں۔
- جمع کریں اور سادہ شکل میں بدلیں۔
اب آپ جانتے ہیں کہ Fractions کو جمع کرنا کیسے ہے! مزید سوالات کے لئے، بلا جھجک پوچھیں۔
یہ بھی پڑھیں: Gestill Tablets: استعمال اور سائیڈ ایفیکٹس
Fractions کو منفی کرنا
جب آپ fractions کو منفی کرتے ہیں، تو یہ سمجھنا ضروری ہے کہ یہ ایک عام ریاضی کا عمل ہے جو آپ کو دو fractions کی تفریق کرنے کے لئے کیا جاتا ہے۔ اس عمل میں کچھ بنیادی اصولوں کو جاننا ضروری ہے۔
1. مشابہ denominators: اگر دونوں fractions کے denominators ایک جیسے ہیں تو یہ عمل نسبتاً آسان ہے۔ مثال کے طور پر:
- ¾ - ¼ = (3 - 1)/4 = 2/4 = ½
2. غیر مشابہ denominators: اگر denominators مختلف ہوں تو پہلے آپ کو انہیں مشابہ بنانا ہوگا۔ اس کے لئے آپ Least Common Denominator (LCD) تلاش کریں:
مثال کے طور پر، fractions ⅖ اور ⅗ پر غور کریں:
- LCD = 5
- تو، ⅖ کو 5 سے ضرب دیں تو یہ 5/5 سے آتا ہے: ⅖ = 5/5 × 2/2 = 4/10
- اسی طرح ⅗ کو 5 سے ضرب دیں گے: ⅗ = 5/5 × 3/3 = 6/10
- اب منفی کریں: 4/10 - 6/10 = -2/10 = -1/5
3. منفی fractions: اگر آپ کی fractions میں سے کوئی ایک منفی ہو، تو نتائج کو برعکس معلوم کرنا ہوگا۔ مثلاً:
- ¾ - (-1/4) = ¾ + 1/4 = 4/4 = 1
غلطیاں سے بچیں: جب آپ fractions کو منفی کرتے ہیں تو یہ چند عام غلطیاں ہیں جو آپ سے ہوسکتی ہیں:
- Denominators کو صحیح نہیں بنانا
- منفی علامات کی غلط فہمی
- جوڑ یا تفریق کرتے وقت صحیح نمبر استعمال نہ کرنا
لہذا، یہ باتیں دھیان میں رکھیں اور بار بار مشق کریں، تاکہ آپ fractions کو منفی کرنے میں ماہر بن سکیں۔ یاد رکھیں کہ صبر اور مشق اس عمل میں کامیابی کی کنجی ہیں!
یہ بھی پڑھیں: How to Unsubscribe Zong Caller Tune in Urdu
Fractions کی ضرب دینا
جب ہم Fractions کی ضرب دیتے ہیں تو یہ بہت سادہ اور واضح عمل ہوتا ہے۔ یہ عمل بہت اہم ہے، کیوں کہ یہ ہمیں مختلف مسائل حل کرنے میں مدد کرتا ہے، جیسے کہ ریاضی، کیمسٹری، اور حیات کی دیگر شاخوں میں۔ تو آئیے جانتے ہیں کہ Fractions کی ضرب کس طرح کی جاتی ہے!
Fractions کی ضرب کرنے کا طریقہ
Fractions کو ضرب دینے کے لئے، آپ کو بس کچھ سادہ قدم اٹھانے ہیں:
- Numerator کو ضرب دیں: پہلے آپ Fractions کے numerator (اوپر والا حصہ) کو آپس میں ضرب دیں۔
- Denominator کو ضرب دیں: پھر، denominator (نیچے والا حصہ) کو بھی آپس میں ضرب دیں۔
- نتیجہ: آخر میں، جو نیا numerator اور denominator ملے گا، اسے ایک نئے Fraction کی صورت میں لکھیں۔
مثال کے طور پر:
فرض کریں کہ ہم یہ Fractions ضرب دینا چاہتے ہیں:
( frac{2}{3} times frac{4}{5} )
اب ہم مندرجہ ذیل مراحل میں عمل کریں گے:
- Numerator: ( 2 times 4 = 8 )
- Denominator: ( 3 times 5 = 15 )
یہاں ہمارے نئے Fraction کا نتیجہ ہوگا:
( frac{8}{15} )
نکات
- یاد رکھیں کہ جب آپ Fractions کی ضرب کر رہے ہوں تو کوئی بھی عدد اگر صفر نہ ہو، تو ہمیشہ سادہ شکل میں تبدیل کریں۔
- چیک کریں کہ کیا آپ کا جواب مزید سادہ کیا جا سکتا ہے۔
یہ تھا Fractions کی ضرب دینے کا سادہ اور مؤثر طریقہ! امید ہے آپ کو یہ معلومات پسند آئیں گی اور آپ اسے اپنے ریاضی کے مسائل حل کرنے میں استعمال کریں گے۔ اگر آپ کے مزید سوالات ہیں، تو بلا جھجھک پوچھیں!
یہ بھی پڑھیں: لوبان کے فوائد اور استعمالات اردو میں
Fractions کی تقسیم کرنا
جب ہم Fractions کی بات کرتے ہیں تو ان کی تقسیم کرنا ایک اہم مہارت ہے۔ بہت سے لوگ ابتدائی طور پر اس عمل میں مشکل محسوس کرتے ہیں، لیکن اگر آپ چند بنیادی قواعد جان لیں تو یہ عمل آسان ہوجاتا ہے۔ آئیے دیکھتے ہیں کہ ہمیں Fractions کی تقسیم کس طرح کرنی ہے۔
کیوں Fractions کی تقسیم ضروری ہے؟
Fractions کی تقسیم مختلف حالات میں استعمال ہوتی ہے۔ مثلاً:
- کھانے کی تقسیم میں، جیسے کہ پیزا یا کیک کو برابر ٹکڑوں میں بانٹنا۔
- سائنس کے تجربات میں، جہاں مختلف مقداروں کو موازنہ کرنا ضروری ہوتا ہے۔
- مالیاتی معاملات میں جیسے کہ سرمایہ کاری کے حصے وغیرہ۔
Fractions کی تقسیم کا طریقہ
Fractions کی تقسیم کرنے کے لئے، آپ کو چند سادہ مراحل پر عمل کرنا ہے:
- Fractions کو یکجا کریں: ایک Fraction کی تقسیم کرنے کے لیے دوسرا Fraction حاصل کریں۔ مثلاً، 2/3 ÷ 4/5۔
- مخالف Fraction حاصل کریں: تقسیم کرنے سے پہلے، دوسرے Fraction کا معکوس لیں۔ یعنی، 4/5 کا معکوس 5/4 ہے۔
- ضرب کریں: اب پہلے Fraction 2/3 کو حاصل کردہ معکوس 5/4 سے ضرب دیں۔ یہ یوں ہوگا:
- نتیجہ حاصل کریں: جب آپ براہ راست ضرب کریں گے، تو آپ کودا نتیجہ ملے گا:
2/3 5/4 = 10/12.
یاد رکھیں کہ آپ کو آخر میں کسی بھی Fraction کو سادہ شکل میں پیش کرنا چاہئے۔ ہمارے نتیجے میں 10/12 کو سادہ کر کے 5/6 حاصل کریں گے۔
مثال:
چلیے ایک اور مثال دیکھتے ہیں:
اگر ہم 1/2 ÷ 3/4 کرنا چاہیں تو:
- 3/4 کا معکوس 4/3 ہوگا۔
- اب آپ 1/2 4/3 کریں گے = 4/6.
- اور 4/6 کو سادہ کر کے 2/3 حاصل کریں گے۔
نیٹجہ: Fractions کی تقسیم کرنا آسان ہے جب آپ اسے صحیح طریقے سے کرتے ہیں۔ تھوڑی سی مشق کے ساتھ، آپ اس مہارت کو بخوبی حاصل کر سکتے ہیں!
مشکل Fractions کے مسائل
جب ہم Fractions کے مسائل کی بات کرتے ہیں، تو کچھ مسائل واقعی چیلنجنگ ہو سکتے ہیں۔ ان مسائل کو حل کرنے کے لیے خاص طریقوں اور سمجھ کی ضرورت ہوتی ہے۔ تو چلیں، اس بلاگ میں ہم کچھ مشکل Fractions کے مسائل دیکھتے ہیں اور ان کے حل کے طریقے سمجھتے ہیں۔
مشکل Fractions کی اقسام
مشکل Fractions کے مسائل کی کئی اقسام ہیں۔ ان میں سے چند اہم ہیں:
- مخلوط Fractions: یہ وہ Fractions ہیں جو پورے نمبر اور Fraction دونوں پر مشتمل ہوتے ہیں۔
- بڑے عددی Fractions: ان میں مقداریں بہت بڑی ہوتی ہیں، جس کی وجہ سے حساب کرنا مشکل ہو جاتا ہے۔
- مختلف denominators کے ساتھ Fractions: جب دو یا زیادہ Fractions کے Denominators مختلف ہوں، تو ان کا جمع یا تفریق کرنا چیلنجنگ ہو سکتا ہے۔
مشکل Fractions کے مسائل کی مثالیں
اب ہم کچھ مثالیں دیکھتے ہیں جو کہ اکثر مشکل سمجھی جاتی ہیں:
| مسئلہ | وضاحت | حل |
|---|---|---|
| 2 3/4 + 1 1/2 | مخلوط Fractions کا جمع کرنا | 3 1/4 |
| 3/5 - 1/4 | مختلف denominators والے Fractions کا تفریق کرنا | 7/20 |
اب ہم ان مسائل کے حل کرنے کے طریقے پر بات کرتے ہیں۔
حل کرنے کے طریقے
مشکل Fractions کے مسائل کو حل کرنے کے لئے درج ذیل مراحل کی پیروی کریں:
- اگر ممکن ہو تو پہلے Fractions کو مخلوط صورت سے سادہ صورت میں تبدیل کریں۔
- جب مختلف denominators ہوں، تو ایک مشترکہ denominator تلاش کریں۔
- پھر Fractions کو جمع یا تفریق کریں۔
- آخر میں جواب کو سادہ شکل میں پیش کریں۔
صبر اور مشق کے ساتھ، آپ ان مشکل Fractions* کے مسائل کو بھی آسانی سے حل کر سکتے ہیں۔ یاد رکھیں، ہر مسئلہ ایک نیا موقع ہے سیکھنے کا!







