Quadratic Equations ریاضی کی ایک بنیادی اصطلاح ہے، جو عموماً دوسری درجہ کی مساواتوں کے حل کی تلاش میں استعمال ہوتی ہے۔ ان مساواتوں کی شکل ax² + bx + c = 0 ہے، جہاں a، b، اور c عددی مستقل ہیں۔ یہ مساواتیں مختلف طریقوں سے حل کی جا سکتی ہیں، جیسے کہ factorization، completing the square، یا quadratic formula کے ذریعے۔
آپ Quadratic Equations کے حل میں ریاضی کی مہارتوں کو استعمال کرتے ہوئے مختلف طریقے آزما سکتے ہیں۔ ان طریقوں کے علم سے نہ صرف آپ اپنے مسائل حل کر سکتے ہیں بلکہ آپ ریاضی کے دیگر شعبوں میں بھی مزید ترقی کر سکتے ہیں۔ ان مساواتوں کا سمجھنا آپ کی تجزیاتی سوچ کو بہتر بنانے میں مددگار ثابت ہوتا ہے۔
Quadratic Equations کے مختلف طریقے
جب ہمیں *Quadratic Equations کو حل کرنے کی ضرورت ہوتی ہے، تو ہمارے پاس مختلف طریقے ہوتے ہیں۔ ان طریقوں کا استعمال موقع پر منحصر ہوتا ہے، یعنی آپ کے سوال کی نوعیت اور مطلوبہ حل کی شکل کیا ہے۔ آئیے ان طریقوں پر ایک نظر ڈالتے ہیں:
1. Factorization کا طریقہ
Factorization ایک عام طریقہ ہے جس کے ذریعے ہم Quadratic Equations کو حل کرتے ہیں۔ اس میں ہم ax² + bx + c = 0 کی صورت میں معادلے کو دو عددی صورت میں لکھتے ہیں۔ مثلاً:
- سب سے پہلے ہمیں coefficients (a, b, c) معلوم ہوتے ہیں۔
- پھر ہم ان کو ایسے دو عوامل میں تقسیم کرتے ہیں جو ضرب میں c کی قدر دیتے ہوں اور جمع میں b کی قدر دیتے ہوں۔
- ایک بار ہم مناسب عوامل تلاش کرلیں، تو ہم دونوں کو صفر کے برابر رکھتے ہیں اور حل کرتے ہیں۔
2. Quadratic Formula کا استعمال
اگر Factorization مشکل ہو تو Quadratic Formula ایک بہترین متبادل ہے۔ یہ فارمولا درج ذیل ہے:
x = (-b ± √(b² - 4ac)) / 2a
اس میں:
- b² - 4ac کو Discriminant کہتے ہیں۔
- اگر یہ صفر ہو تو حل ایک ہو گا، اگر یہ مثبت ہو تو دو مختلف حل ہوں گے، اور اگر یہ منفی ہو تو حقیقی حل نہیں ہو گا۔
3. Completing the Square کا طریقہ
Completing the Square ایک مختلف تکنیک ہے جہاں ہم معادلے کو اس طرح ترتیب دیتے ہیں کہ ایک مکمل مربع بن جائے:
- پہلے ہم ax² + bx + c کو 0 کے برابر کرتے ہیں۔
- پھر ax² + bx کی شکل میں ایک مکمل مربع بناتے ہیں۔
- آخر میں ہم اس مربع کو حل کرتے ہیں۔
4. Graphical Method
اگر آپ گراف کے ذریعے سمجھنا چاہتے ہیں تو Graphical Method بھی ایک دلچسپ طریقہ ہے۔ اس میں آپ Quadratic Equation کے گراف کو بناتے ہیں اور x-axis سے اس کے intersection points کو تلاش کرتے ہیں۔
ان طریقوں میں سے ہر ایک اپنی جگہ مفید ہے، اور آپ کی ضرورت کے مطابق انتخاب کیا جا سکتا ہے۔ آپ کو بس یہ فیصلہ کرنا ہے کہ آپ کے مسئلے کا لئے کون سا طریقہ مناسب رہے گا!
یہ بھی پڑھیں: انگور کے سرکے کے فوائد اور استعمالات اردو میں
Quadratic Equations میں عوامل کا استعمال
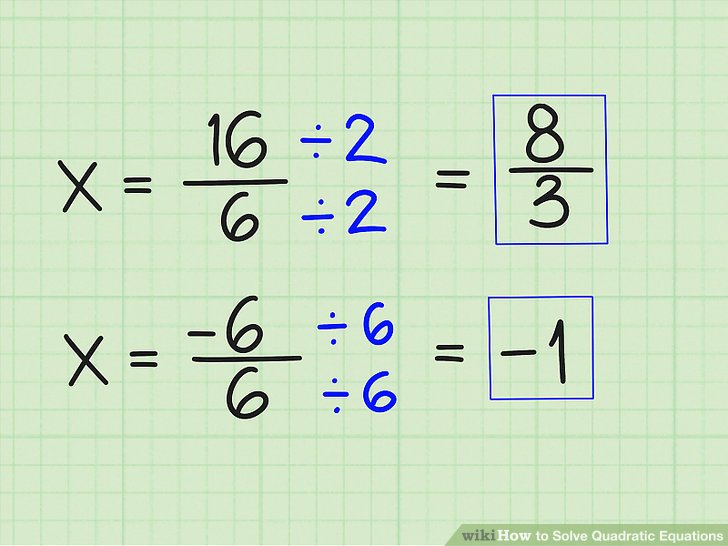
Quadratic Equations کو حل کرنے کا ایک مؤثر طریقہ عوامل کا استعمال ہے۔ یہ طریقہ خاص طور پر ان equations کے لیے مفید ہے جن میں ہم آسانی سے عوامل نکال سکتے ہیں۔ چلیں دیکھتے ہیں کہ یہ عمل کیسے کیا جاتا ہے۔
سب سے پہلے، ایک عام quadratic equation کو دیکھیں:
ax² + bx + c = 0
اس equation میں:
- a = x² کا coefficient
- b = x کا coefficient
- c = constant term
اب ہم عوامل تلاش کرنے کے عمل پر چلتے ہیں۔ مثال کے طور پر، فرض کریں کہ ہمارے پاس quadratic equation ہے:
x² - 5x + 6 = 0
اسے حل کرنے کے لیے ہمیں اس کی factors تلاش کرنے کی ضرورت ہے۔ ہم c (یعنی 6) کے دو ایسے عوامل ڈھونڈیں گے جن کا مجموعہ b (یعنی -5) ہو۔
عوامل جو 6 کو ظاہر کرتے ہیں وہ ہیں:
- 1 اور 6
- 2 اور 3
اب ہمیں ان عوامل کو منفی شکل میں لے جانے کی ضرورت ہے تاکہ ان کا مجموعہ -5 بنے۔ یہاں، ہم -2 اور -3 کا انتخاب کرتے ہیں:
-2 × -3 = 6 اور -2 + -3 = -5
اب ہم factors لکھ سکتے ہیں:
(x - 2)(x - 3) = 0
اب، ہم ہر factor کو صفر کے برابر رکھتے ہیں:
- x - 2 = 0 → x = 2
- x - 3 = 0 → x = 3
اس طرح، ہمیں solutions ملے:
x = 2 اور x = 3
اس عمل کو repeating factors کے ساتھ بھی کیا جا سکتا ہے، لیکن یہ بنیادی طریقہ آپ کو Quadratic Equations کو حل کرنے میں مدد دیتا ہے۔ یاد رکھیں کہ یہ طریقہ صرف ان cases میں مؤثر ہے جہاں آپ factors آسانی سے ڈھونڈ سکیں۔
آپ factors تلاش کرنے کی مشق کرتے رہیں اور جلد ہی آپ quadratic equations کے ماہر بن جائیں گے!
یہ بھی پڑھیں: Cloderm Cream کیا ہے اور کیوں استعمال کیا جاتا ہے – استعمال اور سائیڈ ایفیکٹس
Quadratic Equations کے گرافکس
آپ نے سنا ہوگا کہ Quadratic Equations کے گرافکس، جو کہ parabolas کہلاتے ہیں، فی الفور ہماری بصارت میں آتے ہیں۔ یہ گراف عام طور پر ایک خاص شکل میں ہوتے ہیں اور ان کی کچھ اہم خصوصیات ہوتی ہیں۔ آئیے ان پر ایک نظر ڈالتے ہیں:
- شکل: جب ہم Quadratic Equations کا گراف بناتے ہیں تو ہمیں ایک "U" شکل یا inverted "U" نظر آتا ہے۔ یہ اس بات کا تعین کرتا ہے کہ آیا parabola اوپر کی طرف ہے یا نیچے کی طرف۔
- Vertex: گراف کا سربراہ، جسے ہم vertex کہتے ہیں، اس کی اہمیت بہت زیادہ ہے۔ یہ وہ نقطہ ہے جہاں گراف اپنی سب سے زیادہ یا کم ترین قدر حاصل کرتا ہے۔
- X-Intercepts اور Y-Intercept:
- X-Intercepts وہ نقاط ہیں جہاں گراف X-axis کو چھوتا ہے۔ آپ انہیں حل کرنے کی کوشش کریں تو آپ کو quadratic formula کا استعمال کرنا ہوگا۔
- Y-Intercept وہ نقطہ ہے جہاں گراف Y-axis کو چھوتا ہے، جو کہ ہمیشہ آپ کی equation میں c کی قیمت ہوگی۔
ان گرافکس کی مدد سے ہم مختلف معلومات حاصل کر سکتے ہیں، جیسے کہ solutions کی تعداد اور ان کی نوعیت۔ اگر آپ کا parabola X-axis کو دو نقاط پر چھوتا ہے، تو آپ کے quadratic equation کے دو حقیقی solutions ہیں۔ اگر وہ ایک sola point پر چھوتا ہے تو آپ کا solution ایک ہے اور اگر وہ X-axis کو نہیں چھوتا تو آپ کے solutions تخیلاتی (imaginary) ہوں گے۔
یہ بھی پڑھیں: Clean and Clear Skin Toner کیا ہے اور کیوں استعمال کیا جاتا ہے – استعمال اور سائیڈ ایفیکٹس
Quadratic Equation کی شکل
زیادہ تر Quadratic Equations کو درج ذیل شکل میں لکھا جاتا ہے:
ax² + bx + c = 0
یہاں:
- a = x² کا coefficient
- b = x کا coefficient
- c = constant term
یاد رکھیں، a کبھی بھی صفر نہیں ہوسکتا، ورنہ یہ ایک خطی راستہ (linear equation) میں تبدیل ہوجائے گا۔
گراف کو سمجھنا اور اس کا تجزیہ کرنا Quadratic Equations کے حل میں بہت مددگار ثابت ہوتا ہے۔ اپنی calculations کے ساتھ ساتھ ایک گراف بنانا ہمیشہ ایک بہترین خیال ہے! یہ آپ کو نہ صرف solutions کی صحیح تعداد فراہم کرے گا بلکہ دیگر اہم معلومات بھی فراہم کرے گا۔
Quadratic Equations کی عملی مثالیں
Quadratic equations کو سمجھنے کا بہترین طریقہ عملی مثالوں کے ذریعے ہے۔ آئیں چند اهم عملی مثالوں پر غور کریں:
مثال 1: بنیادی مسئلہ
فرض کریں کہ آپ ایک باغ میں درخت لگانا چاہتے ہیں، اور آپ چاہتے ہیں کہ درختوں کے درمیان کی جگہ ایک خاص شکل میں ہو۔ آپ کا مسئلہ یہ ہے کہ آپ کے پاس 100 میٹر لمبی زمین ہے، اور آپ جاننا چاہتے ہیں کہ اگر آپ درختوں کے درمیان فاصلہ 'x' میٹر مقرر کرتے ہیں تو کتنے درخت لگائے جا سکتے ہیں۔ آپ کا مسئلہ ایسے ہے:
ایکوئیشن:
x² + 10x - 100 = 0
اسے حل کرنے کے لئے، آپ کو Quadratic Formula استعمال کرنا ہوگا:
x = (-b ± √(b² - 4ac)) / 2a
یہاں، a = 1، b = 10، c = -100 ہیں۔ اس کو استعمال میں لاتے ہوئے آپ رکھ سکتے ہیں:
x = (-10 ± √(10² - 4 1 -100)) / 2 1
یہاں سے ہم حل نکال کر دو مختلف جوابات حاصل کر سکتے ہیں۔
مثال 2: زیادہ پیچیدہ مسئلہ
آئیں ایک اور مثال دیکھتے ہیں جو زیادہ پیچیدہ ہے۔ فرض کریں کہ ایک پتنگ ہوا میں اڑ رہی ہے، اور آپ کو پتنگ کی ہلکی ہلکی حرکت کو ماپنا ہے۔ ان پٹ میں دو مختلف پہلو ہیں:
پتنگ کی اونچائی = h میٹر
اسی وقت پتنگ کا Horizontal Distance = d میٹر
ہماری quadratic equation ہوگی:
h = -5d² + 20d + 50
اس میں آپ اپنے مختلف Distance کو رکھ کر پتنگ کی اونچائی جان سکتے ہیں۔ اس کی گراف کی شکل بھی کافی دلچسپ ہوگی۔
نتیجہ
ان مثالوں سے آپ سمجھ سکتے ہیں کہ Quadratic Equations کا استعمال روزمرہ کے مسائل میں کس قدر اہم ہے۔ یہ صرف ایک تصویر پیش کرتی ہیں کہ کیسے ہم اپنی قریب ہونے والی مشکلات کا حل کر سکتے ہیں۔ استعمال کے مختلف طریقے سمجھنے کے ساتھ ساتھ الگ الگ مشقیں کرتے رہنا ضروری ہے۔
