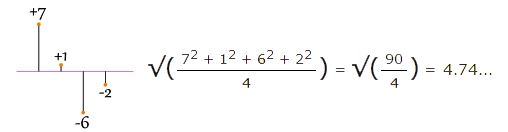معیاری انحراف ایک اہم مفہوم ہے جو سٹیٹسٹکس میں استعمال ہوتا ہے۔ یہ کسی ڈیٹا سیٹ کی تقسیم کی پیمائش کرتا ہے اور ہمیں بتاتا ہے کہ ڈیٹا کے مختلف قیمتیں اوسط سے کتنی دور ہیں۔ معیاری انحراف کا حساب لگانا ڈیٹا میں موجود پراسراریت کو سمجھنے میں مدد کرتا ہے، جو کہ مختلف شعبوں میں بہت زیادہ اہمیت رکھتا ہے، خصوصاً سائنس، مالیات اور انجینئرنگ میں۔
اس مضمون میں، ہم یہ جانیں گے کہ معیاری انحراف کو کیسے تلاش کیا جائے۔ اس کے ساتھ ساتھ ہم مختلف مثالوں اور تکنیکوں کا بھی ذکر کریں گے جو اس عمل کو آسان بناتی ہیں۔ معیاری انحراف کو سمجھنے سے نہ صرف ڈیٹا کی درست تجزیہ میں مدد ملتی ہے بلکہ یہ آپ کو مزید مؤثر فیصلے کرنے کی اجازت بھی دیتا ہے۔
معیاری انحراف کا فارمولا
معیاری انحراف (Standard Deviation) ایک اہم شماریاتی پیمانہ ہے جو اعداد و شمار کے ایک سیٹ کی پھیلاؤ یا انتشار کو ظاہر کرتا ہے۔ جب ہمیں یہ جاننے کی ضرورت ہوتی ہے کہ ہمارے ڈیٹا کی ویلیوز اوسط سے کتنی دور ہیں تو ہم معیاری انحراف کا حساب لگاتے ہیں۔ یہ خاص طور پر ان مواقع پر مفید ہوتا ہے جب آپ کو یہ سمجھنے کی ضرورت ہوتی ہے کہ آپ کے ڈیٹا کا معیار کتنا مستحکم ہے۔
معیاری انحراف کا فارمولا کچھ یوں ہے:
σ = √(Σ(xi - μ)² / N)
یہاں:
- σ = معیاری انحراف
- Σ = مجموعہ، یعنی تمام اجزا کا جمع کرنا
- xi = ہر ایک مشاہدے کی ویلیو
- μ = اوسط (Mean)، تمام مشاہدات کی اوسط کی قدر
- N = مشاہدات کی تعداد، یعنی کتنے ڈیٹا پوائنٹس موجود ہیں
یہ بھی پڑھیں: Qumic 500mg کے فوائد اور سائیڈ ایفیکٹس
معیاری انحراف کے حساب کتاب کا طریقہ
معیاری انحراف کا حساب کیسے لگایا جائے؟ آئیے ایک مثال کے ذریعے سمجھتے ہیں:
- پہلا قدم: اپنی ڈیٹا سیٹ کو جمع کریں۔ فرض کریں کہ ہمارے پاس یہ ویلیوز ہیں: 5، 7، 3، 9، 11۔
- دوسرا قدم: اوسط (Mean) نکالیں: μ = (5 + 7 + 3 + 9 + 11) / 5 = 7
- تیسرا قدم: ہر ویلیو سے اوسط کو منفی کرتے ہوئے، فرق کی مربع بنا لیں:
- (5 - 7)² = 4
- (7 - 7)² = 0
- (3 - 7)² = 16
- (9 - 7)² = 4
- (11 - 7)² = 16
- چوتھا قدم: ان تمام فرق کے مربع کی مجموعہ نکالیں: Sum = 4 + 0 + 16 + 4 + 16 = 40
- پانچواں قدم: اب فارمولا میں رکھیں: σ = √(40 / 5) = √8 ≈ 2.83
اس مثال کے نتائج کو دیکھتے ہوئے، ہم جان سکتے ہیں کہ ہمارے ڈیٹا میں معیاری انحراف تقریباً 2.83 ہے، جو ہمارے ڈیٹا کے پھیلاؤ کو ظاہر کرتا ہے۔ یوں، معیاری انحراف کا یہ طریقہ ہماری مدد کرتا ہے کہ ہم سادہ انداز میں کسی بھی ڈیٹا سیٹ کی تفصیلات کو بہتر سمجھ سکیں۔
یہ بھی پڑھیں: Sunflex Tablet کیا ہے اور اس کے استعمال اور سائیڈ ایفیکٹس
معیاری انحراف کیسے حساب کریں
معیاری انحراف (Standard Deviation) ایک ایسا طریقہ ہے جس کے ذریعے ہم ڈیٹا کی تقسیم میں پھیلاؤ کو جانچ سکتے ہیں۔ یہ ہمیں بتاتا ہے کہ ہمارے ڈیٹا کے نمبروں کی اوسط سے کتنی دوری پر ہیں۔ یہاں ہم آپ کو معیاری انحراف کو حساب کرنے کا طریقہ بتائیں گے۔
1. اوسط کا حساب کریں: سب سے پہلے، آپ کو اپنے ڈیٹا کے نمبروں کا اوسط (Mean) نکالنا ہوگا۔ یہ کرنے کے لیے، آپ تمام نمبروں کا مجموعہ کریں اور ان کی تعداد سے تقسیم کریں۔
مثال:
- نمبرز: 5, 7, 3, 9, 11
- مجموعہ: 5 + 7 + 3 + 9 + 11 = 35
- تعداد: 5
- اوسط: 35 / 5 = 7
2. انحراف کا حساب کریں: اب آپ کو ہر نمبر سے اوسط کو منفی کرنا ہوگا اور اس کی طاقت (Square) لینی ہوگی۔
مثال:
- (5 - 7)² = (-2)² = 4
- (7 - 7)² = 0² = 0
- (3 - 7)² = (-4)² = 16
- (9 - 7)² = 2² = 4
- (11 - 7)² = 4² = 16
اب آپ کے پاس انحراف کی طاقت کے نتائج ہیں: 4, 0, 16, 4, 16۔
3. انحراف کی طاقت کا مجموعہ: اب ان تمام انحراف کی طاقتوں کا مجموعہ نکالیں۔
مثال:
- مجموعہ: 4 + 0 + 16 + 4 + 16 = 40
4. اوسط انحراف کی طاقت کا حساب کریں: اس مجموعہ کو نمبروں کی تعداد میں تقسیم کریں۔
مثال:
- اوسط: 40 / 5 = 8
5. معیاری انحراف نکالیں: آخر میں، اس اوسط کے مربع جڑ (Square Root) لیں۔
مثال:
- معیاری انحراف: √8 = 2.83 (تقریباً)
اور یہ ہے کہ آپ نے معیاری انحراف کو حساب کیا! اس عمل کے ذریعے، آپ کو اپنے ڈیٹا کی موجودگی کی مزید بہتر سمجھ فراہم ہوتی ہے۔
یہ بھی پڑھیں: گوند کِکڑ کے فوائد اور استعمالات اردو میں Gond Kikar
ایک مثال کے ساتھ وضاحت
آئیے ہم معیاری انحراف کو سمجھنے کے لیے ایک حقیقی زندگی کی مثال دیکھتے ہیں۔ فرض کریں کہ آپ نے اپنے سکول کے کلاس کے طلباء کے ایک ٹیسٹ کے نتائج جمع کیے ہیں۔ آپ کے پاس ان طلباء کے نمبر یہ ہیں:
- 80
- 85
- 90
- 70
- 75
- 95
- 85
- 60
- 88
- 92
پہلا قدم ہے کہ ہم ان کی اوسط معلوم کریں۔ یہ کرنے کے لیے، ہم تمام نمبروں کو جمع کریں گے اور طلباء کی تعداد سے تقسیم کریں گے۔
| نمبر | درستگی کے لئے |
|---|---|
| 80 + 85 + 90 + 70 + 75 + 95 + 85 + 60 + 88 + 92 | = 850 |
اب، طلباء کی تعداد 10 ہے۔ تو اوسط:
اوسط = 850 / 10 = 85
اگلا قدم ہے کہ ہمیں ہر نمبر سے اوسط کو منہا کرنا ہے، پھر ان کے مربع لینے ہیں، اور آخر میں ان تمام مربعوں کو جمع کرکے ان کی اوسط نکالنی ہے۔ اس کے بعد ہم اس کے مربع جذر لیں گے تاکہ معیاری انحراف حاصل ہو سکے۔
مثال کے طور پر:
- (80 - 85)² = 25
- (85 - 85)² = 0
- (90 - 85)² = 25
- (70 - 85)² = 225
- (75 - 85)² = 100
- (95 - 85)² = 100
- (85 - 85)² = 0
- (60 - 85)² = 625
- (88 - 85)² = 9
- (92 - 85)² = 49
ان تمام مربعوں کا مجموعہ:
25 + 0 + 25 + 225 + 100 + 100 + 0 + 625 + 9 + 49 = 1129
اب، ہم اس عدد کو طلباء کی تعداد سے تقسیم کرتے ہیں:
1129 / 10 = 112.9
آخری مرحلہ یہ ہے کہ ہم اس کا مربع جذر نکالیں:
معیاری انحراف = √112.9 ≈ 10.63
تو، اس مثال کی روشنی میں، ہم نے دیکھا کہ معیاری انحراف 10.63 ہے۔ یہ عدد ہمیں یہ ظاہر کرتا ہے کہ طلباء کے نمبروں میں کس قدر فرق ہے۔ جتنا زیادہ معیاری انحراف ہوگا، اتنا زیادہ طلباء کے نمبروں میں ویریئنس ہوگی۔
دیگر حوالوں سے معیاری انحراف
معیاری انحراف (Standard Deviation) ایک اہم شماریاتی قدر ہے جو کسی ڈیٹا سیٹ کی منتشر ہونے کی مقدار کو ظاہر کرتی ہے۔ اگر ہم مختلف ذرائع و حوالوں سے معیاری انحراف کو دیکھیں، تو ہمیں اس کی کچھ خاص باتیں معلوم ہوتی ہیں:
- غیر معمولی قیمتوں کا اثر: جب ڈیٹا میں کچھ غیر معمولی قیمتیں ہوتی ہیں، تو معیاری انحراف ان کا درست اندازہ لگانے میں مدد کرتا ہے۔ مثلاً، اگر کسی امتحان میں اکثر طلباء کے نمبر اچھے ہوں، لیکن ایک یا دو طلباء کے نمبر بہت کم ہوں، تو معیاری انحراف ہمیں یہ بتاتا ہے کہ یہ فرق کتنا زیادہ ہے۔
- مفہوم کی وضاحت: جب ہم کسی ڈیٹا سیٹ کا معیاری انحراف جان لیتے ہیں تو ہمیں یہ سمجھنے میں مدد ملتی ہے کہ یہ ڈیٹا اوسط سے کتنا دور ہے۔ یہ معلومات ہمارے لیے اس ڈیٹا سیٹ کی ترتیب سمجھنے میں مفید ہوتی ہے۔
- بین الاقوامی معیار: مختلف تحقیقات اور تجربات میں معیاری انحراف کا استعمال کیا جاتا ہے۔ اس کی مدد سے بین الاقوامی سطح پر ڈیٹا کے موازنے کو آسان بنایا جاتا ہے۔
مثال کے لئے، اگر کوئی کمپنی اپنے پروڈکٹس کی کسٹمر سیٹسفکشن کا جائزہ لیتی ہے، تو معیاری انحراف ان کی خدمات یا پروڈکٹس کی معیار کو جانچنے میں مدد کرتا ہے۔ یہ جاننے کے لیے کہ گاہکوں کی رائے میں کتنی ورائیٹی ہے، یہ ایک موثر ذریعہ ہے۔
معیاری انحراف کا حساب: دیگر حوالوں کے ساتھ
| ماخذ | مفہوم |
|---|---|
| تعلیمی اشاعتیں | سٹوڈنٹس کے گریڈ کے فرق کو جانچنے کے لیے استعمال ہوتا ہے۔ |
| مالیاتی رپورٹس | مارکیٹ میں سرمایہ کاری کے خطرات کا تجزیہ کرنے میں مدد کرتا ہے۔ |
| سائنسی تحقیق | ڈیٹا کے تجرباتی نتائج کے اعتبار کو جانچنے میں معاونت کرتا ہے۔ |
یہ تمام حوالہ جات ہمیں یہ سمجھنے میں مدد دیتے ہیں کہ معیاری انحراف کی بنیاد پر مختلف شعبوں میں ڈیٹا کا تجزیہ کیسے کیا جا سکتا ہے اور یہ معلومات کی تحقیق کے لئے کتنا ضروری ہے۔ ہم یہ بھی دیکھتے ہیں کہ اگرچہ معیاری انحراف ایک عددی قیمت ہے، لیکن اس کی تشریح مختلف مسائل میں مختلف ہو سکتی ہے۔
