How to Calculate Half Life of First Order Reaction in Urdu

پہلی آرڈر کی ردعمل کی Half Life کی پیمائش کرنا کیمیائی ردعمل کی رفتار کو سمجھنے کے لیے ایک اہم عمل ہے۔ جب کوئی کیمیائی ترکیب پہلی آرڈر کی درجہ بندی میں آتا ہے، تو اس کی رفتار براہ راست مواد کی مقدار کے ساتھ جڑی ہوتی ہے۔ اس کا مطلب ہے کہ ردعمل کی رفتار میں تبدیلی اس کی ابتدائی کنسنٹریشن پر منحصر ہے۔

Half Life کا حساب کرنا ایک سادہ فارمولا کے ذریعے کیا جا سکتا ہے، جو کہ کیمیائی ردعمل کے دوران وقت کے ساتھ مواد کی بقا کی پیمائش کرتا ہے۔ اس کی درستگی کو یقینی بنانے کے لیے مختلف عوامل کو مدنظر رکھنا ضروری ہے، جیسے درجہ حرارت اور دباؤ، جو ردعمل کی رفتار کو متاثر کر سکتے ہیں۔

پہلی آرڈر کی کیمیائی ردعمل کی خصوصیات

پہلی آرڈر کی کیمیائی ردعمل میں کچھ اہم خصوصیات ہیں جو اسے دیگر ردعمل کی اقسام سے ممتاز کرتی ہیں۔ ان خصوصیات کو سمجھنا کیمیاء کے طلباء اور ماہرین کے لیے ضروری ہے۔ آئیے ان خصوصیات پر ایک نظر ڈالتے ہیں:

• ردعمل کی رفتار: پہلی آرڈر کے ردعمل کی رفتار صرف reactant کی مقدار پر منحصر ہوتی ہے۔ اگر reactant کی مقدار بڑھتی ہے تو ردعمل کی رفتار بھی بڑھتی ہے۔
• نصف زندگی (Half Life): پہلی آرڈر کے ردعمل کی نصف زندگی مستقل ہے اور یہ reactant کی ابتدائی مقدار پر منحصر نہیں ہوتی۔ یہ ایک اہم خاصیت ہے کیونکہ نصف زندگی ہر وقت ایک ہی رہتی ہے۔
• تجزیاتی شکل: پہلی آرڈر ردعمل کی ریاضیاتی شکل یہ ہے:

  ln[A]t = -kt + ln[A]0

  جہاں [A]t وقت t پر reactant کی مقدار ہے، k ردعمل کی رفتار کا مستقل ہے، اور [A]0 ابتدائی مقدار ہے۔

• درجہ حرارت کا اثر: درجہ حرارت کے ساتھ ردعمل کی رفتار میں تبدیلی آتی ہے، اور یہ Arrhenius قانون کے مطابق کیمیائی تبدیلیوں کا اثر ڈالتا ہے۔
• استحکام: پہلی آرڈر کے ردعمل عام طور پر زیادہ مستحکم ہوتے ہیں اور ان کی شرحیں دیگر اقسام کے بالمقابل زیادہ رکھی جا سکتی ہیں۔

یہ خصوصیات پہلی آرڈر کے ردعمل کو نہ صرف سادہ بلکہ قابل سمجھ بھی بناتی ہیں۔ یہ خاص طور پر سائنسی تجربات، فارماسیوٹیکلز اور کیمیائی انجینئرنگ میں انتہائی اہم ہیں۔ پہلی آرڈر کی کیمیائی ردعمل کی خاصیتوں کی تفہیم سے ہمیں مختلف شیمیکل پروسیسز کے بارے میں بہتر طور پر سمجھنے کا موقع ملتا ہے۔

آخر میں، یہ کہنا مناسب ہوگا کہ پہلی آرڈر کی کیمیائی ردعمل کی خصوصیات ان کے مطالعہ کو انتہائی دلچسپ بناتی ہیں۔ جیسے جیسے ہم اس پروگرام کے دوسرے پہلوؤں پر جائیں گے، آپ کو مزید معلومات ملیں گی جو آپ کے تجربات میں مددگار ثابت ہوں گی۔

یہ بھی پڑھیں: How to Check the Owner of SIM in Urdu

Half Life کا فارمولا

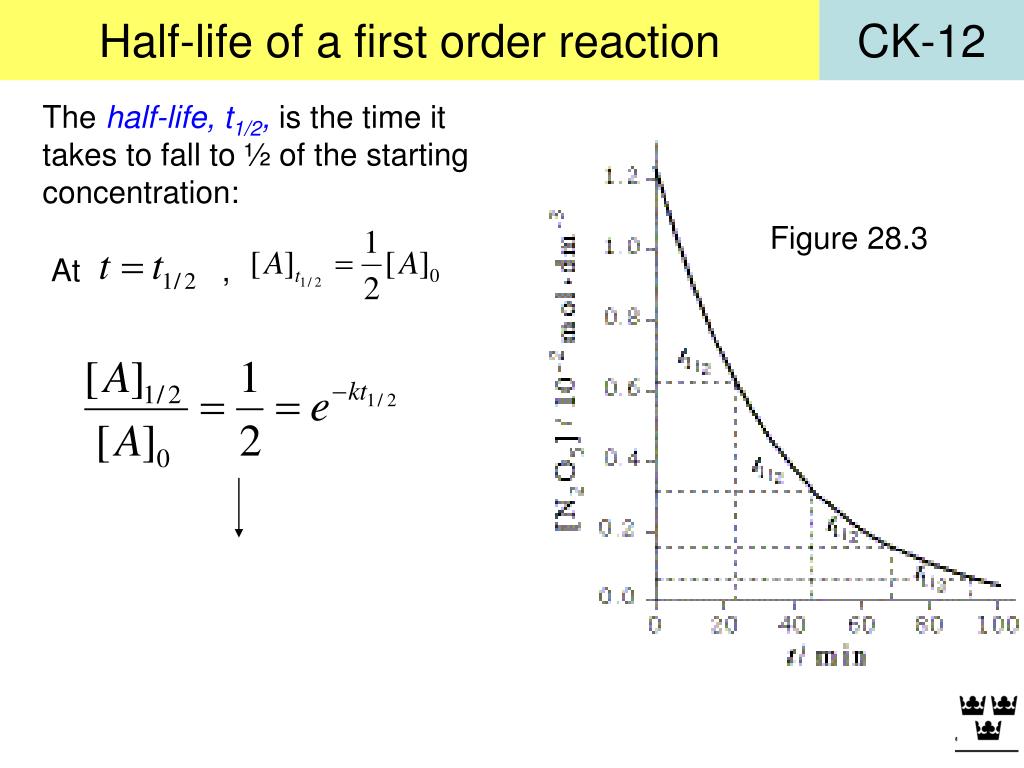
جب ہم Half Life کی بات کرتے ہیں تو اس کا مطلب ہے کہ کسی مادے کی تعداد یا مقدار آدھی ہو جانے کے لئے درکار وقت۔ یہ سائنسی اصطلاح خاص طور پر ریڈیو ایکٹو مادوں، ادویات، اور کیمیکلز کے لیے استعمال ہوتی ہے۔ *Half Life کا فارمولا یہ سمجھنے میں مدد کرتا ہے کہ یہ عمل کیسے کام کرتا ہے۔

آسان الفاظ میں، اگر k کی قیمت بڑھتی ہے تو Half Life* کم ہو جائے گی، یعنی مادہ تیزی سے ختم ہوگا۔ اور اگر k کی قیمت کم ہے تو مادہ آہستہ آہستہ ختم ہوگا۔

اسی طرح، Half Life کا فارمولا مختلف کیمیکلز اور ادویات کی گتھیوں کو سمجھنے میں مدد دیتا ہے، خاص طور پر جب ہمیں معلوم کرنا ہو کہ کسی دوا کی مؤثریت کب تک رہے گی یا کوئی مادہ کب تک محفوظ رہے گا۔

یاد رکھیں کہ یہ حسابات مختلف سائنسی تجربات اور مطالعے کے نتائج کی بنیاد پر بھی مخصوص دائرہ کار رکھتے ہیں، اور مختلف مادے کی خصوصیات کے مطابق ان میں فرق آ سکتا ہے۔

یہ بھی پڑھیں: فرتی ایم انجکشن کے استعمالات اور فوائد اردو میں

Half Life کی حساب کتاب کا عمل

جب ہم کسی مواد کی Half Life کی بات کرتے ہیں تو ہمارا یہ جاننا ضروری ہوتا ہے کہ یہ وقت کی ایک ایسی مدت ہے جس میں ایک مخصوص مقدار نصف رہ جاتی ہے۔ یہ سائنسی اصول مختلف شعبوں میں استعمال ہوتا ہے، خاص طور پر کیمیاء، طبی سائنس، اور نیوکلیئر فزکس میں۔ آئیے دیکھتے ہیں کہ ہم Half Life کی حساب کتاب کیسے کر سکتے ہیں۔

کیا ہمیں Half Life کی ضرورت ہے؟

Half Life کی حساب کتاب کرنے کا مقصد یہ جاننا ہے کہ کوئی مادی جز کس حد تک کمزور ہو جائے گا وقت کے ساتھ۔ چاہے وہ دوا ہو یا نیوکلیئر مادہ، یہ جاننا اہم ہے۔

Half Life کا فارمولا

Half Life (T½) کا حساب لگانے کے لیے ایک سادہ فارمولا استعمال ہوتا ہے:

T½ = (ln(2)) / k

جہاں:

• ln(2): قدرتی لوگریم (natural logarithm) کی ایک مستقل مقدار ہے, جو تقریبا 0.693 ہے۔
• k: یہ کیمیائی ردعمل کی رفتار کی مستقل (rate constant) ہوتی ہے۔

Half Life کی حساب کتاب کے مراحل

1. انتخاب کریں: سب سے پہلے آپ کو یہ طے کرنا ہوگا کہ آپ کس مادی جز کی Half Life معلوم کرنا چاہتے ہیں۔
2. شرح رفتار حاصل کریں: اس کیمیائی یا نیوکلیئر ردعمل کی شرح رفتار (k) معلوم کریں۔
3. فارمولا اپنائیں: اوپر دیا گیا فارمولا استعمال کریں۔ ln(2) کی قیمت کو 0.693 کے ساتھ تبدیل کریں۔
4. نتیجہ نکالیں: آخر میں، حساب کتاب کریں اور یہ طے کریں کہ Half Life کی قدر کیا ہے۔

ایک مثال

فرض کریں کہ ایک مادہ کی شرح رفتار k = 0.1 دن^-1 ہے۔ تو اس کی Half Life کی حساب کتاب کچھ اس طرح ہوگی:

T½ = (0.693) / (0.1) = 6.93 دن

یعنی، اس مادے کی Half Life تقریباً 6.93 دن ہے۔

امید ہے کہ اب آپ کو Half Life کی حساب کتاب کرنے کا عمل سمجھ آ گیا ہوگا! اگر آپ کے مزید سوالات ہیں تو بلا جھجھک پوچھیں۔

یہ بھی پڑھیں: How Many Meals Do Japanese Eat a Day in Urdu

مثال کے ذریعے وضاحت

پہلی آرڈر کے ردعمل کی Half Life کا حساب کرنا ایک دلچسپ لیکن تھوڑا سا پیچیدہ عمل ہو سکتا ہے۔ چلیں، ایک مثال کے ذریعے اسے سمجھتے ہیں۔ فرض کریں کہ ہمارے پاس ایک کیمیکل ری ایکشن ہے جو پہلی آرڈر کی مذہب رکھتا ہے۔ اس کی رفتار کا قانون یہ ہے:

Rate = k [A]

جہاں k ری ایکشن کی رفتار کا مستقل ہے اور [A] ری ایکٹینٹ کی مقدار ہے۔ پہلی آرڈر کی خاصیت یہ ہے کہ اس کی Half Life، ابتدائی مقدار پر منحصر نہیں ہوتی۔

یہ بھی پڑھیں: Lorys Garlic Hair Cream: استعمال اور سائیڈ ایفیکٹس

مثال:

آئیے فرض کرتے ہیں کہ ہمارے پاس 100 moles کا ری ایکٹینٹ A ہے اور اس کا رفتار مستقل k = 0.693 min^-1 ہے۔ ہمیں اس کا Half Life (t_1/2) معلوم کرنا ہے۔ اس کا حساب لگانے کا فارمولہ یہ ہے:

t_1/2 = 0.693 / k

اب ہم اس فارمولے میں k کی قیمت شامل کرتے ہیں:

t_1/2 = 0.693 / 0.693 min^-1

اسے حل کرنے پر ہمیں:

t_1/2 = 1 minute

وضاحت:

اس کا مطلب یہ ہوا کہ 100 moles کی مقدار کو 1 منٹ کے اندر آدھا ہو جائے گا۔ یوں اگر ہم 1 منٹ بعد چیک کریں گے، تو ہمیں 50 moles نظر آئیں گے۔ اگر ہم اس عمل کو دوبارہ دہرائیں، تو 2 منٹ میں 25 moles باقی رہیں گے، اور اسی طرح یہ مقدار وقت کے ساتھ ساتھ آہستہ آہستہ کم ہوتی جائے گی۔

آخر میں، یہ یاد رکھیں کہ پہلی آرڈر کے ردعمل کی خاصیت ہے کہ Half Life مستقل رہتا ہے چاہے ہم ابتدائی مقدار کو کوئی بھی رکھیں۔ یہ اس کے حساب کو آسان بناتا ہے اور کیمیکل انجینئرنگ اور سائنسی تحقیق کے لیے ایک اہم تصور ہے۔

اس مثال کو سمجھنے کے بعد، آپ جلدی سے Half Life کا حساب کر سکتے ہیں، جو کہ کیمیکل ری ایکشن کی رفتار کو جاننے میں مددگار ثابت ہوگا۔